If someone doesn’t understand how to do math and doesn’t have a reason to try, chances are they won’t bother. There’s nothing more discouraging than a struggle that feels unnecessary. For that reason, math intimidates many non-math majors.

Professor David Nacin’s new book is meant to change all that. “Math Infused Sudoku” is a new take on the classic puzzle that adds clues about sums, differences, means, divisibility and more.

“My goal is to expose people to math in such a way that feels fun and it’s a game, but they might secretly end up learning more math than they would ever expect from the rules of the puzzle,” Nacin said. “It’s about the gamification of math.”

Nacin never liked Sudoku because although it has numbers in it, the numbers could be replaced by letters or symbols, and it wouldn’t affect the outcome of the puzzle. There are no actual math operations involved.

“The idea behind the book is that I was gonna make the numbers matter,” Nacin said. “I want all of the clues to involve the actual numbers themselves.”

A classic Sudoku puzzle has nine rows and 81 squares (cells). Nacin’s book has nine chapters and 81 puzzles.

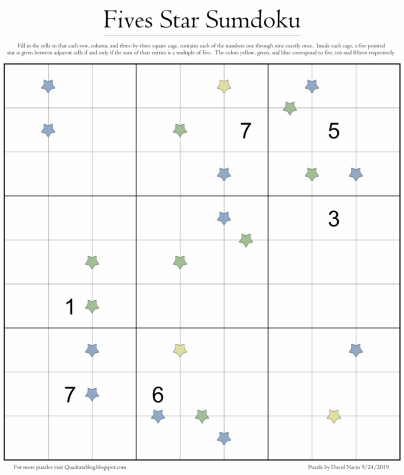
Each chapter introduces a new type of Sudoku puzzle. The different types have different clues. For example, in a “Sumdoku,” the clues indicate the sums of numbers entered into certain cells.

The puzzles in the final chapter of “Math Infused Sudoku” incorporate the clue types of all the previous chapters. There’s also fewer and fewer clues as the book progresses.

Some of the puzzles offered in the book are also featured on Nacin’s blog, “Quadrata,” where he regularly posts puzzles. “Quadrata” is the Latin word for square. A “Latin square” is a set of rows and columns where a number can only appear once in each row or column.

Nacin has been making his own math puzzles for about 7 years. He was inspired by Brian Hayes of the math and computer science blog Scientific American, who created a puzzle using complex numbers (such as “i,” the square root of -1).

Hayes made it because he’d never seen anything like it before; Nacin hadn’t, either.

“Basically [Hayes] said, ‘I’m not sure whether the solution I found is unique, or whether there’s a good process for solving it,'” Nacin said. “And I said I was gonna keep working on it until I was the first one to ever find a way to [find a unique solution].”

Nacin is also part of the Math Horizons and Focus magazines.

Though he thoroughly enjoys making puzzles that incorporate higher-level math, such as number theory and group theory, Nacin designed “Math Infused Sudoku” with accessibility in mind.

“I want to make them accessible to people,” he said. “I want as many people as possible to be able to do them.”

Nacin gives his students puzzles in class as extra credit, but doesn’t make them mandatory because he doesn’t want to penalize anyone for not liking puzzles.

“So if they’re practicing in number theory and I give them a number theory puzzle, they’d have to lots of different calculations,” he said. “It’ll be something from their number theory class and there’ll be all these different things that they have to fill in.”

There are other professors in William Paterson’s math department who have assigned their students puzzles from Nacin’s book.

Last Wednesday, a student from Boston University emailed Nacin to let him know that his professor used puzzles from “Math Infused Sudoku” in her class. She also showed students Nacin’s “Quadrata” blog.

Creating puzzles that have only one solution is a challenge.

“If you just randomly put down clues, you’re probably gonna get a puzzle that has no solution, or too many solutions,” Nacin said. “And when people do puzzles, they wanna find the solution – so if you have a puzzle that has two solutions, it’s no good.”

Finding the circumstances when a solution is unique is a whole area of study in mathematics.

Nacin double-checks that his puzzles have a unique solution by doing them himself, sending them through a computer programming software called Python, checks them himself again and then sends them to the magazine that will publish them.

“Sometimes when they change the graphics, they leave out one of the clues, so I always double-check after they do the graphics,” he said. “I’ve had that happen at least twice.”

Nacin said he comes up with new kinds of puzzles whenever he gets “too good” at the ones he currently does.

“If I do the same puzzle for too long, I’ll start to get too good at it,” he said. “So I’ll always have to make new ones, in order to keep throwing myself off balance.”

Nacin, who specializes in non-commutative algebra, got his Ph.D. from Rutgers University and went straight to teaching at William Paterson University.

He originally wanted to be a computer programmer and was intimidated by the amount of math it required. But after some time in the major, he fell in love with math and switched majors.

“I like that there’s the absolute truth and false [in math],” Nacin said. “I like that you have reproducible results. It’s not something you can argue with. That’s one of the things I love about math, the absolute truth.”